Absolute-value problems

Consider how the absolute value of a real number x relates to a fixed positive number, say 4:
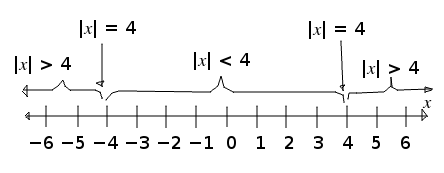
Graph of |x| versus 4.
On the inside is one region where |x| < 4, on the outside are two regions where |x| > 4, and these regions are separated by two points where |x| = 4. Using this picture it's easy to solve these equation and inequalities:
This statement …has this solution.
|x| < 4; −4 < x < 4.
|x| > 4; x < −4 or x > 4.
|x| = 4; x = −4 or x = 4.
This works in much greater generality.

Inequalities with absolute values

The general principles for solving inequalities with absolute vales are actually a bit simpler than the general principle for solving equations, so I'll start with inequalities.

Here are the relevant rules:

This statement … is equivalent to this statment.
|a| < b; −b < a < b.
|a| ≤ b; −b ≤ a ≤ b.
|a| > b; a < −b or a > b.
|a| ≥ b; a ≤ −b or a ≥ b.

These pairs of statements are equivalent for any real numbers a and b, whether positive, negative, or zero. This means that you can substitute any expressions, however complicated, for a and b above, and the equivalence will be valid. For the examples in this class, we'll typically use a linear expression for a and a constant for b; then the statement on the right will be one that you already know how to solve.

For example, here's an inequality where the absolute value of a linear expression is less than a constant:

And here's one where the absolute value of a linear expression is greater than a constant:

Here's an example with a weak inequality; notice that it uses the same rule as for a strict inequality:

There are also some degenerate problems along this line. Here's an example:

You can solve this problem very quickly if you remember that an absolute value is never negative, so it couldn't possibly be less than −4. Even if you don't notice this, however, and go through the steps anyway, still they won't send you astray as long as you do them correctly. But when you get to the end, you should notice that the compound inequality is never true; a graph can really help here.

Equations with absolute values

The general rule for an equation with an absolute value is a bit complicated:
This statement … is equivalent to this statment.
|a| = b; a = −b or a = b, and b ≥ 0.
Fortunately, when you replace b by a constant, it's obvious whether the last condition is true or not. So normally you just have to look at two possibilities.

Here's an example to show what I mean:

Normally, you wouldn't even bother to write down the bit about 7 ≥ 0; since you can see right away that this is true, you go on directly to the next step. Here's an example where I do just that:

Still, you do have to think about that bit; compare this example:

If I'd forgotten to check whether −5 ≥ 0 and just pressed on with the two equations, then I'd have gotten −1 and 4 as solutions, but these are wrong. (If you put them in for x in |2x − 3|, you'll get 5, not −5.) Again, if you remember that an absolute value can never be negative, then you won't fall into this trap!

Another way to think about this is that you replace the equation |a| = b with the compound statement a = b or a = −b, but you might get extraneous solutions. So in the previous example, I could solve 2x − 3 = 5 or 2x − 3 = −5, getting x = −1 or x = 4, but then I would have to check these solutions. Since they both make the original statement come out false, they're extraneous, so there are no solutions in the end.

Isolating the absolute value

The rules above only apply directly if the absolute value is alone on one side of the equation or inequality. If this is not so, then you can still solve it, but you first have to isolate the absolute value.

To do this, pretend that the absolute value is itself a single thing (don't pay any attention for now to what's inside it), and this thing is the variable that you're solving for.

For example:

Here, I had to add 5 to both sides to get the absolute value alone, just like I would have done if I'd wanted to solve x − 5 = 7.

Here's another example:

This time the first step —to divide by 3— is the same as it would be to solve 3x ≤ 12.

Equating two absolute values

You might also see an equation with two (or even more) absolute values in it! In general, this can be a quite complicated affair; first, you have to isolate one absolute value and get rid of it, then (in every statement that results) you have to isolate the other absolute value and get rid of it. In principle, you can always do it, but it can be a big mess!

However, if you simply want to say that the two absolute values are equal, then there is a short cut that makes everything much easier. The reason is that two real numbers have the same absolute value exactly when they are either equal or opposite:

This statement … is equivalent to this statment.
|a| = |b|; a = b or a + b = 0.

For example:

This is a little more complicated than the other examples on this page, because the same steps won't solve both equations; you really have to treat them separately. But you can do it.

Occasionally you can get a degenerate one of these too. For example:

So usually there are two solutions, one for each equation; but sometimes there may be only one (if one equation is always false), or everything may be a solution (if one equation is always true, for example |5 − y| = |y − 5|).
Go back to the course homepage.
This web page and the image in it were written between by Toby Bartels, last edited on 2020 November 12. Toby reserves no legal rights to them.

The permanent URI of this web page is http://tobybartels.name/MATH-1100/2020FA/absolute/.

HTML 5