Functions (§§3.1&3.2)

As I stated in the introduction, we will use a lot of functions in this class. Functions are an important type of mathematical object, along with relations, sets, and constant numbers.

Relations and functions

There are many different types of mathematical objects that we could study in this class. Some of them are relation-like objects:

truth values,
sets,
relations,
ternary relations,
etc;

some of them are function-like objects:

constants,
functions,
binary functions,
ternary functions,
etc.

As you go along these lists, both the number of variables and the number of dimensions needed for graphing increase, as in the following diagram:

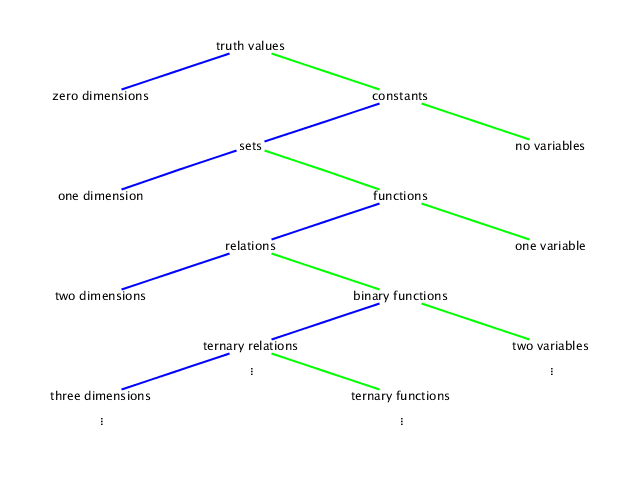
A truth value is either true or false; any statement with no variables in it, such as the statement that 0 < 2, should evaluate to true or false (in this case, true).

A constant is, in this class, usually a real number, such as −2. Any expression with no variables should evaluate to a constant, but we use one dimension to graph a constant on a number line.

A set is, in this class, a set of real numbers. A statement with one variable defines a set, such as {x | x < 2}, the set of real numbers that are less than 2. We again use one dimension to graph a set.

A function, or unary function for emphasis, is a rule for taking one number (the input, or argument) and using it to calculate a number (the output, or value). An example is (x ↦ x − 2), the rule which subtracts 2 from any number. To graph a function, we need two dimensions, one for the input and one for the output.

A relation, or binary relation for emphasis, is a set of ordered pairs instead of a set of individual numbers. An example is {x, y | x + y < 2}. We again use two dimensions to graph a relation.

We can continue with binary functions, ternary functions, etc, which take two or more numbers as inputs; and we can continue with ternary relations, quaternary relations, etc, which relate three or more numbers. But we will not actually study these in this class.

Names of functions

Just as we can use a variable to stand for a constant, so we can use variables to stand for sets, relations, and functions. For example, if A stands for the set {x | x < 2}, then these two statements mean the same thing:

x ∈ A, usually pronounced ‘x in A’;
x < 2.

The first of these says that x belongs to the set A, while the second uses the definition of A to say exactly what that means. Similarly, if f stands for the function (x ↦ x − 2), then these two expressions mean the same thing:

f(x), usually pronounced ‘f of x’;
x − 2.

The first of these is the value of the function f at the argument x, while the second uses the definition of f to say exactly what that means.

One of the basic principles of the theory of functions is that the only information necessary to specify a function is to show how to calculate its value at any argument. Therefore, if I write

f(x) = x − 2

and state that this holds for every real number x, then I have completely specified the function f. Usually in class (and always in the book), we will define a function with a name, but really it's just another way of saying that f is the function (x ↦ x − 2). It's a handy method, because you have an equation in which you can replace x with any other expression (since the equation holds for every real number x). For example, using the function f above, we can replace x with 5 to calculate that

f(5) = (5) − 2 = 3.

Or we can say that

f(2x + 3) = (2x + 3) − 2 = 2x + 1.

Notice that I always put parentheses around an expression when I substitute it for a variable; in this case, it wasn't really necessary, but it's best to play it safe.

Graphs of functions

Every function can be thought of as a relation, specifically

{x, y | y = f(x)}.

Conversely, if a relation is given by an equation in x and y and you can solve this equation for y, then the relation can be thought of as a function. In the graph, this corresponds to the Vertical Line Test:

A graph of a relation is the graph of a function if and only if every vertical line goes through the graph at most once.

Sometimes a vertical line doesn't go through the graph at all! This happens when f(x) is undefined. The domain of f is the set of all inputs where f is defined:

dom f = {x | f(x) exists}.

Along with the domain, we can also consider the range, which is the set of all outputs of the function; however, calculating that from a formula will be easier after we discuss inverse functions (§6.2).

Go back to the course homepage.

This web page was written between 2010 and 2013 by Toby Bartels, last edited on 2013 October 14. Toby reserves no legal rights to it. The diagram was drawn with the aid of Jacques Distler's SVG editor.

The permanent URI of this web page is http://tobybartels.name/MATH-1150/2013FA/functions/.