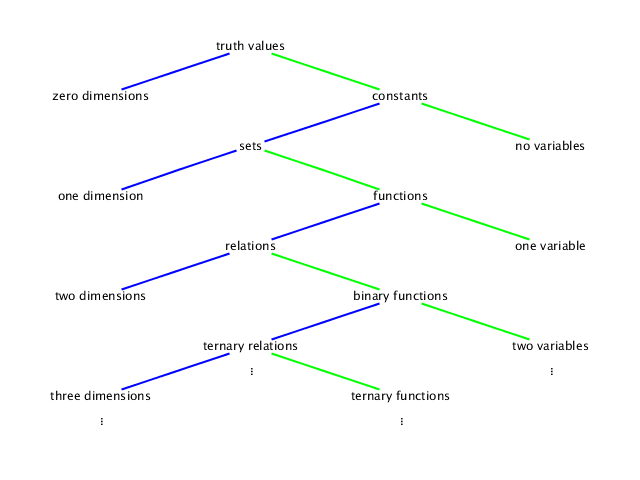
A truth value is either true or false; any statement with no variables in it, such as the statement that 0 < 2, should evaluate to true or false (in this case, true).
A constant is, in this class, a real number, such as −2. Any expression with no variables should evaluate to a constant, but we use one dimension to graph a constant on a number line.
A set is, in this class, a set of real numbers. A statement with one variable defines a set, such as {x | x < 2}, the set of real numbers that are less than 2. We again use one dimension to graph a set.
A function, or unary function for emphasis, is a rule for taking one number (the input, or argument) and using it to calculate a number (the output, or value). An example is (x ↦ x − 2), the rule which subtracts 2 from any number. To graph a function, we need two dimensions, one for the input and one for the output.
A relation, or binary relation for emphasis, is a set of ordered pairs instead of a set of individual numbers. An example is {x, y | x + y < 2}. We again use two dimensions to graph a relation.
A binary function, or function of two variables, is a rule for taking an ordered pair of two inputs and using it to calculate an output. An example is (x, y ↦ x + y − 2), the rule which subtracts 2 from the sum of the two inputs. To graph a binary function, we need three dimensions, two for the inputs and one for the output.
A ternary relation, or relation between three variables, is a set of ordered triples instead of a set of ordered pairs. An example is {x, y, z | x + y + z < 2}. We again use three dimensions to graph a ternary relation.
A ternary function, or function of three variables, is a rule for taking an ordered triple of three inputs and using it to calculate an output. An example is (x, y, z ↦ x + y + z − 2), the rule which subtracts 2 from the sum of the three inputs. To graph a ternary function, we need four dimensions, three for the inputs and one for the output.
A quaternary relation, or relation between four variables, is a set of ordered quadruples. An example is {x, y, z, A | x + y + z + A < 2}. We again use four dimensions to graph a quaternary relation.
We can continue with quaternary functions, quinary functions, etc, which are functions of four or more variables; and we can continue with quinary relations, senary relations, etc, which are relations between five or more variables. (But around this point, most people stop using the ‘‑ary’ terms, because few people can remember them.)
The permanent URI of this web page
is
http://tobybartels.name/MATH-2080/2013SP/functions/.