Simplifying polynomials
If you combine the techniques of the previous two lectures,
you can simplify any polynomial.
(Remember the polynomials can involve
both addition
and multiplication between non-constant expressions.)
Multiplying by a monomial
The simplest new sort of problem
is probably multiplication of a polynomial by a monomial.
For example,
consider the expression x2(x3 + 5).
If this x2 were a constant,
then you'd know to use the distributive law
and multiply each of the terms x3 and 5 by that constant.
Well, the distributive law sitll works the same way;
you still multiply each of those terms, but now by x2.
However, to multiply x3 by x2,
you can use an exponential identity to simplify this to x5.
Thus, the result is x5 + 5x2.
Here are a few examples, including some degenerate cases:
- x2(x3 + 5) ≡
x2 · x3 +
x2 · 5 ≡
x5 + 5x2;
- x2(x + 5) ≡
x2 · x +
x2 · 5 ≡
x3 + 5x2;
- x(x3 + 5) ≡
x · x3 +
x · 5 ≡
x4 + 5x;
- x(x + 5) ≡
x · x + x · 5 ≡
x2 + 5x;
Really, all of these are essentially the same,
but some of them use the identity x ≡ x1
at some point.
Here is a slightly more complicated family of examples,
where I have to multiply some constants as well:
- 3x2(2x3 + 5) ≡
3x2 · 2x3 +
3x2 · 5 ≡
6x5 + 15x2;
- 3x2(2x3 − 5) ≡
3x2 · 2x3 +
3x2 · (−5) ≡
6x5 − 15x2;
- −3x2(2x3 + 5) ≡
−3x2 · 2x3 −
3x2 · 5 ≡
−6x5 − 15x2;
- −3x2(2x3 −
5) ≡
−3x2 · 2x3 −
3x2 · (−5) ≡
−6x5 + 15x2;
Notice how I have (−) · (−) = (+)
in the last example.
Doubling the distributive law
Consider the expression (t + 2)(t + 3).
This is a polynomial, made up using only addition and multiplication,
but it may not be obvious how to remove the parentheses and simplify it.
If it were t(t + 3),
then you could use the distributive law
to turn it into t2 + 3t,
and if it were (t + 2)3,
then you could use the distributive law on the other side
to turn it into 3t + 6.
How can you deal with the full expression
(t + 2)(t + 3)?
The answer is to use the distributive law on both sides.
First, treat the factor t + 3 as a single expression,
ignoring that it can be broken down as a sum.
Then you can use the distributive law on the factor t + 2
to get t(t + 3) + 2(t + 3).
That done, now you can use that t + 3 is a sum
and apply the distributive law in the other direction
(twice, in fact, once for each term)
to get t2 + 3t + 2t + 6,
which simplifies (by combining terms)
to t2 + 5t + 6.
Let's see that again, slowly:
- (t + 2)(t + 3) —
original expression
- t(t + 3) + 2(t + 3) —
use the distributive law (on the right)
to distribute t + 3 to both t and 2;
- (t · t + t · 3) +
(2 · t + 2 · 3) —
use the distributive law (on the left)
to distribute t to both t and 3,
and again to distribute 2 to both t and 3;
- (t2 + 3t) +
(2t + 6) —
simplify each monomial term;
- t2 +
(3t + 2t) + 6 —
rearrange order of addition;
- t2 + (3 + 2)t + 6 —
use the distributive law backwards to combine like terms;
- t2 + 5t + 6 —
since 3 + 2 is 5.
Probably the most important step to understand in the list above
is the long one:
(t · t + t · 3) +
(2 · t + 2 · 3).
The parentheses here aren't important
—they just tell you to add the terms in a specific order,
which doesn't make any difference—
but they're helpful to keep track of where each term comes from.
The first pair comes from multiplying t by both t and 3,
while the second pair comes from multiplying 2 by both t and 3.
In other words, to simplify (t + 2)(t + 3),
both t and 2 are multiplied by both t and 3.
This is just one example of the general rule:
Multiply each term by each term.
That is, when multiplying one polynomial (a sum of monomial terms)
by another polynomial (another sum of monomial terms),
multiply each term of the first polynomial
by each term of the second polynomial.
These multiplications, of course,
use the monomial techniques from the last lecture;
afterwards, you combine like terms
using the techniques from the lecture before.
Here are some more examples.
In each case, the first step
involves multiplying each term by each term,
the second step uses monomial techniques to simplify each product term,
the next step rearranges the order of addition of the terms,
and the last step combines like terms to get the final answer.
Try to get good enough at this
that you only need to write down every other formula
(the original expression, the middle expression, and the final result).
- (t + 2) (t + 3) ≡
(t · t + t · 3) +
(2 · t + 2 · 3) ≡
(t2 + 3t) +
(2t + 6) ≡
t2 + (3t + 2t) + 6 ≡
t2 + 5t + 6;
- (4t + 2) (5t + 3) ≡
(4t · 5t + 4t · 3) +
(2 · 5t + 2 · 3) ≡
(20t2 + 12t) +
(10t + 6) ≡
20t2 +
(12t + 10t) + 6 ≡
20t2 + 22t + 6;
- (4t − 2) (−5t + 3) ≡
(4t · −5t +
4t · 3) +
(−2 · −5t +
−2 · 3) ≡
(−20t2 + 12t) +
(10t − 6) ≡
−20t2 +
(12t + 10t) − 6 ≡
−20t2 + 22t − 6;
- (x2 + 4x − 2)
(3 − 5x) ≡
(x2 · 3 +
x2 · −5x) +
(4x · 3 +
4x · −5x) +
(−2 · 3 +
−2 · −5x) ≡
(3x2 − 5x3) +
(12x − 20x2) +
(−6 + 10x) ≡
−5x3 +
(3x2 − 20x2) +
(12x + 10x) − 6 ≡
−5x3 −
17x2 + 22x − 6;
- (x + xy) (y + 3) ≡
(x · y + x · 3) +
(xy · y +
xy · 3) ≡
(xy + 3x) +
(xy2 + 3xy) ≡
xy2 +
(xy + 3xy) + 3x ≡
xy2 +
4xy + 3x.
Powers of polynomials
Since you know the identities
(ab)n ≡
anbn
and (a + b)c ≡
ac + bc,
you might think that there is a similar identity
for (a + b)n.
There is not!
Actually, if you study sufficiently advanced algebra,
you might learn an identity, but it's this:
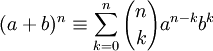
I mention this not so that you can use it
—you won't have any need to use it in this course!—
but just to make it as clear as I can to you
that you have no useful identity
for (a + b)n.
How then
should you simplify an expression like (x + 2)2?
The wrong answer would be x2 + 4;
instead you should turn the exponentiation into multiplication
and use the techniques above:
- (x + 2)2 — original expression
- (x + 2)(x + 2) —
rewritten using multplication;
- (x2 + 2x) +
(2x + 4) —
multiply each term by each term;
- x2 + 4x + 16 —
combine like terms.
If you have (x + 2)3 (or more),
then you simply multiply over and over again:
- (x + 2)3 — original expression
- (x + 2)(x + 2)(x + 2) —
rewritten using multplication;
- (x2 + 4x +
16)(x + 2) —
using previous calculation of (x + 2)(x + 2);
- (x3 +
4x2 + 16x) +
(2x2 + 8x + 32) —
multiply each term by each term;
- x3 + 6x2 +
24x + 32) —
combine like terms.
Eventually if you do enough of these,
then you might start to see a pattern,
which is ultimately the pattern summarised
in the big scary identity from the beginning of this section.
But we're not going to get into that in this course.
Go back to
the MATH-0950-ES32
homepage.
This web page was written in 2007 by Toby Bartels.
The image on this web page
was made in 2007 by Toby Bartels
using texvc.
Toby reserves
no legal rights to either of them.
The permanent URI of this web page
is
http://tobybartels.name/MATH-0950/2007SP/polynomials/.